A CUDA Quick Reference. For corrections or improvements, just leave a comment.
Download Cuda Cheatsheet
(Version: July 05, 2012)
Donnerstag, 5. Juli 2012
Dienstag, 29. Mai 2012
Kleine Linksammlung ([GP]GPU, Hardware)
CUDA
CUDA Webinars (Online Präsentationen zu CUDA und GPGPU Techniken):
http://developer.nvidia.com/cuda/cuda-education-training
Zur GT300/GF100 bzw. Fermi Architektur
http://www.nvidia.com/object/GTX_400_architecture.html
http://www.computerbase.de/artikel/grafikkarten/2010/bericht-nvidia-gf100-technische-details/4/#abschnitt_streaming_multiprocessor_sm
Artikel zur GTX 470/480 und Fermi-Architektur
("Vergleich" mit ATi HD5870)
http://www.tweakpc.de/hardware/tests/grafikkarten/nvidia_geforce_gtx_480/s02.php
CUDA und OpenCL Vergleich und Missverständnisse
http://www.streamcomputing.eu/blog/2011-06-22/opencl-vs-cuda-misconceptions/
CUDA Supported GPUs:
http://en.wikipedia.org/wiki/CUDA#Supported_GPUs
GPGPU/CUDA Einführung, Workflow (ausführliche Informationen mit Tipps&Tricks)
http://www.moderngpu.com/intro/performance.html
http://www.moderngpu.com/intro/workflow.html
Nomenklatur Nvidia GeForce
- http://en.wikipedia.org/wiki/GeForce#Nomenclature
- http://forums.nvidia.com/index.php?showtopic=226700&st=40
- http://www.pcgameshardware.de/aid,775478/Nvidia-Nach-Fermi-folgen-Kepler-und-Maxwell/Grafikkarte/News/
OpenGL / DirectX
Warum DirectX inzwischen so verbreitet ist, obwohl OpenGL mindestens wenn nicht sogar bessere Chancen hatte:
+ http://www.joystiq.com/2009/05/22/dubious-marketing-microsoft-makes-directx-9-look-really-bad/
Artikel contra OpenGL
http://www.tomshardware.com/reviews/opengl-directx,2019-10.html
Gegenüberstellung einiger Features für OpenGL und DirectX
http://rastergrid.com/blog/2011/10/opengl-vs-directx-the-war-is-far-from-over/
Sonstiges
Maxwell GPUs mit ARM Rechenkerne (2011 kaufte Nvidia ARM Lizenzen, siehe auch Nvidia Tegra):
http://www.heise.de/newsticker/meldung/Nvidia-bestaetigt-Auf-Maxwell-GPUs-sitzen-auch-ARM-Prozessorkerne-1172923.html
http://www.streamcomputing.eu/blog/2012-04-18/usb-stick-sized-arm-computers/
http://www.itproportal.com/2011/06/20/intel-pushes-hpc-space-knights-corner/
http://www.pcwelt.de/ratgeber/Die-wichtigsten-ARM-Prozessoren-4159343.html
[...]
CUDA Webinars (Online Präsentationen zu CUDA und GPGPU Techniken):
http://developer.nvidia.com/cuda/cuda-education-training
Zur GT300/GF100 bzw. Fermi Architektur
http://www.nvidia.com/object/GTX_400_architecture.html
http://www.computerbase.de/artikel/grafikkarten/2010/bericht-nvidia-gf100-technische-details/4/#abschnitt_streaming_multiprocessor_sm
Artikel zur GTX 470/480 und Fermi-Architektur
("Vergleich" mit ATi HD5870)
http://www.tweakpc.de/hardware/tests/grafikkarten/nvidia_geforce_gtx_480/s02.php
CUDA und OpenCL Vergleich und Missverständnisse
http://www.streamcomputing.eu/blog/2011-06-22/opencl-vs-cuda-misconceptions/
CUDA Supported GPUs:
http://en.wikipedia.org/wiki/CUDA#Supported_GPUs
GPGPU/CUDA Einführung, Workflow (ausführliche Informationen mit Tipps&Tricks)
http://www.moderngpu.com/intro/performance.html
http://www.moderngpu.com/intro/workflow.html
Nomenklatur Nvidia GeForce
Die Namensgebung von Nvidia ist äußerst "interessant". Anbei ein paar Auflistungen zur möglichen Entwirrung.
Hinweise: Die Bezeichnung der Chiparchitektur müssen nicht immer mit den Modellbezeichnungen 1-zu-1 übereinstimmen. Auch bedeutet eine höhere Modellnummer nicht automatisch bessere Technik. Neuauflagen (Rebranding) älterer Grafikchips sind zu berücksichtigen. So verwenden die GTS 240/250 noch den G92b Chip, während sonst die Geforce 200 Serie auf GT2xx Chip basiert. Modelle wie GT 320 verwenden noch den
GT2xx Chip. Die GT 330 verwendet sogar noch den G92b Grafikchip.
Geforce 9 Modelle wurden später einfach umbenannt und finden sich als GT 1xx wieder. Die Umbenennung schließt die Lücke zwischen der 9er Serie und der nachfolgenden GT200 Architektur, wenn ich das richtig verstanden habe. Eine Geforce 9500 GT heißt dann Geforce GT 120. GT200 ist dann als Nachfolger die eigentliche Tesla Architektur und entsprechende Modelle heißen bspw. GT 240 oder GTX 285. Der Grafikchip GT300 führt die Fermi Architektur ein und begründet wieder eine neue Kodierung: GF100. Analog bei der Kepler Architektur mit GK100. Mit der GT100er/200er Serie kommt generell ein neues Bezeichnungsschema für die GPU-Modelle zum Einsatz:
- G oder kein Suffix – Low-Budget
- GT – Mainstream
- GTS – Performance
- GTX – High-End
| CUDA Generation | Codename | Grafikchip | Beispielmodelle |
| 1 | (Unified Shader Architecture) | G80, G92[b], G94, G96[b], G98 | Geforce 8800GT, Geforce 9800GT, ..., siehe auch Geforce 100 Serie |
| 2 | Tesla | GT200[b], GT215, GT216, GT218 | GT 240, GTX 285, ...; GT320, GT 340, ...; Tesla C1060 (Geforce 405) |
| 3 | Fermi | GF100, GF104, GF106, GF108; GF110, GF114,... |
GT 440, GTX 470; GT 520, GTX 570, GTX 580; GT 605, GT 620, GT 645 |
| 4 | Kepler | GK104, GK107, GK108, GK114,... | GT 630, GTX 670, GTX 680, GTX 690 |
| 5 (>=2013) | Maxwell |
- http://en.wikipedia.org/wiki/GeForce#Nomenclature
- http://forums.nvidia.com/index.php?showtopic=226700&st=40
- http://www.pcgameshardware.de/aid,775478/Nvidia-Nach-Fermi-folgen-Kepler-und-Maxwell/Grafikkarte/News/
OpenGL / DirectX
Warum DirectX inzwischen so verbreitet ist, obwohl OpenGL mindestens wenn nicht sogar bessere Chancen hatte:
API use was shifted in favor of DirectX by Microsoft's two-pronged DirectX campaign around the launch of XBox 360 and Windows Vista, including the spread of FUD (fear, uncertainty and doubt) about the future of OpenGL, and wild exaggeration of the merits of DirectX. Ever since then, the network effects have amplified this discrepency until OpenGL has almost disappeared entirely from mainstream PC gaming.http://blog.wolfire.com/2010/01/Why-you-should-use-OpenGL-and-not-DirectX
+ http://www.joystiq.com/2009/05/22/dubious-marketing-microsoft-makes-directx-9-look-really-bad/
Artikel contra OpenGL
http://www.tomshardware.com/reviews/opengl-directx,2019-10.html
Gegenüberstellung einiger Features für OpenGL und DirectX
http://rastergrid.com/blog/2011/10/opengl-vs-directx-the-war-is-far-from-over/
Sonstiges
Maxwell GPUs mit ARM Rechenkerne (2011 kaufte Nvidia ARM Lizenzen, siehe auch Nvidia Tegra):
http://www.heise.de/newsticker/meldung/Nvidia-bestaetigt-Auf-Maxwell-GPUs-sitzen-auch-ARM-Prozessorkerne-1172923.html
http://www.streamcomputing.eu/blog/2012-04-18/usb-stick-sized-arm-computers/
http://www.itproportal.com/2011/06/20/intel-pushes-hpc-space-knights-corner/
http://www.pcwelt.de/ratgeber/Die-wichtigsten-ARM-Prozessoren-4159343.html
[...]
Mittwoch, 11. April 2012
Linux/Kubuntu - Qt + Cuda + QtCreator
"Cuda Toolkit 4.1 and Qt4 on Linux"
Content:
1. GPU Drivers + CUDA Toolkit 4.1 + CUDA SDK
2. QtCreator and Qt4 Example Project with CUDA
3. Compile Qt4 from scratch (optional)
4. Tools - Debugging and Profiling
--
My System:
- Kubuntu 11.10 (Oneiric Ocelot) at 32bit.
- g++ v4.5, gcc v4.5 (4.6 and up is not supported by cuda toolkit 4.1, see here)
- Qt 4.7.4 (dev-tools, qtcreator)
Downloads:
- Cuda Toolkit 4.1 + SDK (got Ubuntu 11.04 & 32bit)
- qt4_mandelbrot (Qt4 example project with Cuda kernel)
--
1. Get the NVidia / CUDA stuff installed:
I've got here:
cudatoolkit_4.1.28_linux_32_ubuntu11.04.run
gpucomputingsdk_4.1.28_linux.run
1.1 Drivers
First of all we update our nvidia drivers. After I got some troubles with the downloaded drivers (blue colored videos^^) the following did it for me.
sudo add-apt-repository ppa:ubuntu-x-swat/x-updates
sudo apt-get update
sudo apt-get install nvidia-current
Now I have NVidia driver version 295.40.
(Refs: wiki.ubuntuusers.de, hecticgeek)
1.2 Toolkit
Just run:
sudo ./cudatoolkit_4.1.28_linux_32_ubuntu11.04.run
Edit your .bashrc:
export PATH=/usr/local/cuda/bin:$PATH
export LD_LIBRARY_PATH=/usr/local/cuda/lib:$LD_LIBRARY_PATH
1.3 NVIDIA GPU COMPUTING SDK
To install the gpu computing sdk, just run as user:
./gpucomputingsdk_4.1.28_linux.run
The examples are not build yet, you actually have to run make in ~/NVIDIA_GPU_Computing_SDK, but in most cases errors will occur.
Error Messages:
"unsupported GNU version! gcc 4.6 and up are not supported!",
Install gcc-4.5 and g++-4.5 as a second compiler and softlink to it in /usr/local/cuda/bin
sudo ln -s /usr/bin/gcc-4.5 /usr/local/cuda/bin/gcc
rendercheck_gl.cpp:(.text+0x119b): undefined reference to 'gluErrorString'
cannot find -lcuda
Lib paths are messed up in common.mk and common_cudalib.mk (see here). Path to nvidia_current is missing. I have uploaded a patched version.
Download Patch
Maybe you have to edit the path to your nvidia driver where libcuda and others are located. Edit in that downloaded patch the files common.mk and common_cudalib.mk at the beginning:
# ### patch for finding libcuda
NVIDIA_CURRENT = /usr/lib/nvidia-current/
There are still some errors in the freeImageInteropNPP in CUDALibraries, but I dont care for the moment. The examples can be compiled in NVIDIA_GPU_Computing_SDK/C/ directly. I run deviceQuery to check if installation was successfull.
~/NVIDIA_GPU_Computing_SDK/C/bin/linux/release$ ./deviceQuery
If this is working for you, then everything with cuda is fine. If you got "./deviceQuery: error while loading shared libraries: libcudart.so.4: cannot open shared object file: No such file or directory", then you forgot to add the cuda libs to LD_LIBRARY_PATH.
--
2. Qt4 Projects with CUDA on Linux
Start your QtCreator and create a new project (or download qt4_mandelbrot as example). My structure is:
qt4_mandelbrot - source code
qt4_mandelbrot/obj - object code including cuda object code
qt4_mandelbrot/bin - binaries
// I've disabled the shadow build option in the qt4 project settings, because I configured the directories in the .pro file on my own.
For the .pro file cuda settings I refer to this site. You also can have a look at the qt4_mandelbrot project.
In QtCreator you need to set the build environment. Go to Projects and add to the Build Environment a new variable "LD_LIBRARY_PATH" with "/usr/local/cuda/lib". Check if the execution environment has this setting as well.
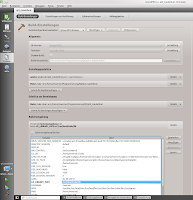
Press Ctrl+B or Ctrl+R to build/run the project.
--
3. Qt4 - compile it from scratch (optional)
Downloads:
- Qt Environment (Download Page)
- - Qt Sourcecode (tar.gz) (v4.8.1)
- - Qt Creator (32bit Binary, v2.4.1)
untar source code:
tar -xf qt-everywhere-opensource-src-4.8.1.tar.gz
configure Qt for compilation ("-release", "-shared" are actually default)
./configure -release -shared -no-qt3support -no-webkit -optimized-qmake -no-multimedia -no-phonon -nomake examples -nomake demos
compile and install (takes a while, runs with two jobs at once cuz I have two CPUs):
sudo make install -j2
install qt creator
chmod +x qt-creator-linux-x86-opensource-2.4.1.bin
./qt-creator-linux-x86-opensource-2.4.1.bin
start qt creator and set path to qmake (Qt Creator - Tools - Options: Qt Versions):
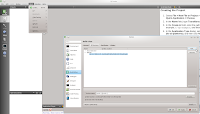
Now you can try a qt application created by the project wizard of Qt Creator. Press Ctrl+R to compile and run.
To get access to Qt on shell/console, you have to extend the PATH variable. Edit .profile and .bashrc (home directory) and add:
export PATH=/usr/local/Trolltech/Qt-4.8.1/bin/:$PATH
Uninstall:
Qt: cd /pathto/qt_source and sudo make uninstall
QtCreator: cd /pathto/qtcreator/ and run ./uninstall
--
4. Tools - Debugging and Profiling
For debugging you can try DDD (sudo apt-get install ddd):
ddd --debugger cuda-gdb ./application
If you just have a single GPU you can't debug local kernels yet. Since NSight 2.2 enables Single-GPU debugging again (NSight is only for Windows/VisualStudio), I hope the upcoming Toolkit 4.2 will do this for Linux as well.
For informations on memory leaks and access errors just use cuda-memcheck (see manual ;) ).
Profiling:
To profile the gpu site you can use the nvidia profiler (nvvp). Just run nvvp and open your binary into a new session.
References:
http://stackoverflow.com/...cuda-incompatible-with-my-gcc-version
http://developer.nvidia.com/cuda-toolkit-41
http://wiki.ubuntuusers.de/Grafikkarten/Nvidia
http://www.hecticgeek.com/...drivers-in-ubuntu-11-10-oneiric-ocelot/
http://forums.developer.nvidia.com/...compiling-sdk-on-ubuntu-11-10/p1
http://qt.nokia.com/downloads
http://cudaspace.wordpress.com/...qt-creator-cuda-linux
http://www.gnu.org/s/ddd/
http://oprofile.sourceforge.net/about/
http://doc.opensuse.org/...tuning.oprofile.html
http://lbrandy.com/...oprofile-profiling-in-linux-for-fun-and-profit/
It is time for another tutorial. Today we want to setup Qt+Cuda on Linux/Kubuntu. It is recommend to install Qt from the repositories. In the 3rd section I also wrote down the instructions for compiling Qt from scratch. If you find some oddities, just leave a comment (this isn't the best HowTo, I am still learning).
Content:
1. GPU Drivers + CUDA Toolkit 4.1 + CUDA SDK
2. QtCreator and Qt4 Example Project with CUDA
3. Compile Qt4 from scratch (optional)
4. Tools - Debugging and Profiling
--
My System:
- Kubuntu 11.10 (Oneiric Ocelot) at 32bit.
- g++ v4.5, gcc v4.5 (4.6 and up is not supported by cuda toolkit 4.1, see here)
- Qt 4.7.4 (dev-tools, qtcreator)
Downloads:
- Cuda Toolkit 4.1 + SDK (got Ubuntu 11.04 & 32bit)
- qt4_mandelbrot (Qt4 example project with Cuda kernel)

--
1. Get the NVidia / CUDA stuff installed:
I've got here:
cudatoolkit_4.1.28_linux_32_ubuntu11.04.run
gpucomputingsdk_4.1.28_linux.run
1.1 Drivers
First of all we update our nvidia drivers. After I got some troubles with the downloaded drivers (blue colored videos^^) the following did it for me.
sudo add-apt-repository ppa:ubuntu-x-swat/x-updates
sudo apt-get update
sudo apt-get install nvidia-current
I've uninstalled all the nvidia drivers before, but maybe you don't have to. I did a backup of my /etc/X11/xorg.conf and stopped the x-server (ctrl+alt+F1 and sudo stop kdm, then purging my old nvidia stuff, then run the commands from above and finally sudo start kdm to get back, I hope you wont need to do that).
Now I have NVidia driver version 295.40.
(Refs: wiki.ubuntuusers.de, hecticgeek)
1.2 Toolkit
Just run:
sudo ./cudatoolkit_4.1.28_linux_32_ubuntu11.04.run
Edit your .bashrc:
export PATH=/usr/local/cuda/bin:$PATH
export LD_LIBRARY_PATH=/usr/local/cuda/lib:$LD_LIBRARY_PATH
1.3 NVIDIA GPU COMPUTING SDK
To install the gpu computing sdk, just run as user:
./gpucomputingsdk_4.1.28_linux.run
The examples are not build yet, you actually have to run make in ~/NVIDIA_GPU_Computing_SDK, but in most cases errors will occur.
Error Messages:
"unsupported GNU version! gcc 4.6 and up are not supported!",
Install gcc-4.5 and g++-4.5 as a second compiler and softlink to it in /usr/local/cuda/bin
sudo ln -s /usr/bin/gcc-4.5 /usr/local/cuda/bin/gcc
rendercheck_gl.cpp:(.text+0x119b): undefined reference to 'gluErrorString'
cannot find -lcuda
Lib paths are messed up in common.mk and common_cudalib.mk (see here). Path to nvidia_current is missing. I have uploaded a patched version.
Download Patch
Maybe you have to edit the path to your nvidia driver where libcuda and others are located. Edit in that downloaded patch the files common.mk and common_cudalib.mk at the beginning:
# ### patch for finding libcuda
NVIDIA_CURRENT = /usr/lib/nvidia-current/
There are still some errors in the freeImageInteropNPP in CUDALibraries, but I dont care for the moment. The examples can be compiled in NVIDIA_GPU_Computing_SDK/C/ directly. I run deviceQuery to check if installation was successfull.
~/NVIDIA_GPU_Computing_SDK/C/bin/linux/release$ ./deviceQuery
If this is working for you, then everything with cuda is fine. If you got "./deviceQuery: error while loading shared libraries: libcudart.so.4: cannot open shared object file: No such file or directory", then you forgot to add the cuda libs to LD_LIBRARY_PATH.
--
2. Qt4 Projects with CUDA on Linux
Start your QtCreator and create a new project (or download qt4_mandelbrot as example). My structure is:
qt4_mandelbrot - source code
qt4_mandelbrot/obj - object code including cuda object code
qt4_mandelbrot/bin - binaries
// I've disabled the shadow build option in the qt4 project settings, because I configured the directories in the .pro file on my own.
For the .pro file cuda settings I refer to this site. You also can have a look at the qt4_mandelbrot project.
In QtCreator you need to set the build environment. Go to Projects and add to the Build Environment a new variable "LD_LIBRARY_PATH" with "/usr/local/cuda/lib". Check if the execution environment has this setting as well.

Press Ctrl+B or Ctrl+R to build/run the project.
--
3. Qt4 - compile it from scratch (optional)
Downloads:
- Qt Environment (Download Page)
- - Qt Sourcecode (tar.gz) (v4.8.1)
- - Qt Creator (32bit Binary, v2.4.1)
untar source code:
tar -xf qt-everywhere-opensource-src-4.8.1.tar.gz
configure Qt for compilation ("-release", "-shared" are actually default)
./configure -release -shared -no-qt3support -no-webkit -optimized-qmake -no-multimedia -no-phonon -nomake examples -nomake demos
compile and install (takes a while, runs with two jobs at once cuz I have two CPUs):
sudo make install -j2
install qt creator
chmod +x qt-creator-linux-x86-opensource-2.4.1.bin
./qt-creator-linux-x86-opensource-2.4.1.bin
start qt creator and set path to qmake (Qt Creator - Tools - Options: Qt Versions):

Now you can try a qt application created by the project wizard of Qt Creator. Press Ctrl+R to compile and run.
To get access to Qt on shell/console, you have to extend the PATH variable. Edit .profile and .bashrc (home directory) and add:
export PATH=/usr/local/Trolltech/Qt-4.8.1/bin/:$PATH
Uninstall:
Qt: cd /pathto/qt_source and sudo make uninstall
QtCreator: cd /pathto/qtcreator/ and run ./uninstall
--
4. Tools - Debugging and Profiling
For debugging you can try DDD (sudo apt-get install ddd):
ddd --debugger cuda-gdb ./application
If you just have a single GPU you can't debug local kernels yet. Since NSight 2.2 enables Single-GPU debugging again (NSight is only for Windows/VisualStudio), I hope the upcoming Toolkit 4.2 will do this for Linux as well.
For informations on memory leaks and access errors just use cuda-memcheck (see manual ;) ).
Profiling:
To profile the gpu site you can use the nvidia profiler (nvvp). Just run nvvp and open your binary into a new session.
You can profile (the host site) with gprof or oprofile. gprof needs the compiler flag -pg that is also available in nvcc. Just have a look at the .pro file coming with this tutorials example project. To get a profile you have to run the binary, which creates a gmon.out for the gprof profiler. Now you can generate a readable output:
gprof ./qt4_mandelbrot > output.txt
oprofile (sudo apt-get install oprofile oprofile-gui).
"OProfile is a system-wide profiler for Linux systems, capable of profiling all running code at low overhead. [...] OProfile leverages the hardware performance counters of the CPU [...]" (oprofile website)
So oprofile offers CPU and hardware based profiling which gprof doesn't. For usage I just refer to this site. If you want to read more about the sampling methods and the advantages of oprofile, so read this site.
gprof ./qt4_mandelbrot > output.txt
oprofile (sudo apt-get install oprofile oprofile-gui).
"OProfile is a system-wide profiler for Linux systems, capable of profiling all running code at low overhead. [...] OProfile leverages the hardware performance counters of the CPU [...]" (oprofile website)
So oprofile offers CPU and hardware based profiling which gprof doesn't. For usage I just refer to this site. If you want to read more about the sampling methods and the advantages of oprofile, so read this site.
References:
http://stackoverflow.com/...cuda-incompatible-with-my-gcc-version
http://developer.nvidia.com/cuda-toolkit-41
http://wiki.ubuntuusers.de/Grafikkarten/Nvidia
http://www.hecticgeek.com/...drivers-in-ubuntu-11-10-oneiric-ocelot/
http://forums.developer.nvidia.com/...compiling-sdk-on-ubuntu-11-10/p1
http://qt.nokia.com/downloads
http://cudaspace.wordpress.com/...qt-creator-cuda-linux
http://www.gnu.org/s/ddd/
http://oprofile.sourceforge.net/about/
http://doc.opensuse.org/...tuning.oprofile.html
http://lbrandy.com/...oprofile-profiling-in-linux-for-fun-and-profit/
Labels:
compile,
cuda,
cuda toolkit 4.1,
debug,
install,
kubuntu 11.10,
linux,
make,
mandelbrot,
ocelot,
opengl,
profile,
qt
Mittwoch, 22. Februar 2012
Rectangle Free Grid Coloring - 21x12 and 18x18 Grid With Four Colors
As Steinbach already has posted his solution on Computational Complexity, I give an eye compatible version here ...
18x18 Grid With Four Colors


Rectangle Free Four Coloring of 18x18 Grid, found by B. Steinbach and C. Posthoff
21x12 Grid With Four Colors


Rectangle Free Four Coloring of 21x12 Grid, found by B. Steinbach and C. Posthoff
 For a given complete bipartite graph K(m,n) you have to color its edges with c (e.g. c=4) colors. If you find a coloring such that there is no monochromatic rectangle in K(m,n) then you will have a rectangle free c-coloring of K(m,n). A grid is defined by the adjacency matrix of K(m,n). Each element is a number that indicates the edge color. Figures from above represents such a matrix with m=21 rows and n=12 columns. There are no four points forming a same colored rectangle such as you can see on the right figure.
For a given complete bipartite graph K(m,n) you have to color its edges with c (e.g. c=4) colors. If you find a coloring such that there is no monochromatic rectangle in K(m,n) then you will have a rectangle free c-coloring of K(m,n). A grid is defined by the adjacency matrix of K(m,n). Each element is a number that indicates the edge color. Figures from above represents such a matrix with m=21 rows and n=12 columns. There are no four points forming a same colored rectangle such as you can see on the right figure.
The Zarankiewicz-Problem is a subproblem of the Grid Coloring Problem. Zarankiewicz asks for the minimum number of edges you have to insert into an empty bipartite graph such that there will be formed a rectangle as subgraph. Due to the pigeonhole principle the number of monochromatic edges of one color has to meet [mn/c] in the wanted four-coloring. If it does not then the Grid will not be c-colorable without monochromatic rectangles. Hence you have to solve the Zarankiewicz Problem for disproving a c-coloring of a grid.
B. Steinbach was able to solve the last open problems in the class of four-colorings (17x17, 17x18, 18x17, 18x18, 21x12), so he also found the bipartite Ramsey Number BR(2,4)=19 (similar to Ramsey Numbers, just take complete bipartite graphs with monochromatic bicliques). He worked together with Christian Posthoff on these problems. I was lucky to take part in this progress, even though I only was a witness. On one day I asked Bernd Steinbach again, if he had found some new results on the four coloring of the 21x12 problem. I knew that he again subjected a SAT solver to a very deep interrogation on the previous day. So Steinbach was speaking without any emotion about fifteen minutes that everything had been failed, what actually was the normal answer as always, and he finished with a little smile: "then he (SAT solver) got it".
First we really had our doubts and we were about to develop algorithms to prove that there could not be any 4-coloring. Well, my doubts were derived from Steinbach, admittedly I had no idea how to solve this problem. B. Steinbach created a very special sub-solution, which involved an ordered solution of the 21x12 Zarankiewicz-Problem, of course.
But the sub-solution was much more complicated. Steinbach explained it to me on the same day, but the "head" of that sub-solution looked very chaotic to me. After I understood I was stunned again by the system of chaos. O.k., I have to stop here for the sake of fairness. Steinbach will publish all the details on it soon but it will take some time. He did a great work, you will like it.
--
I have been playing around with the 21x12 solution to find the relationship between the color classes and the reduced latin squares of order 4, according to the Zarankiewicz Problem (see my upcoming paper). You will recognize the structure in the following pictures:




Each color class has been sorted, I use always the red color for the sake of readability. You also can see the Slot Architecture (matrix head (4,4,4) partition). The next figures show the structure of the four reduced latin squares in the adjacency matrix. One 3-bit pattern has to be expanded to three 2-bit patterns (see my upcoming paper).




As I worked out in my paper, the position of the last bits (highlighted) can be written in a tableau with four rows and four columns, so the Reduced Latin Squares of Order 4 are obtained:

The last three reduced latin squares belong to the same isotopy class (also isomorphic in this case, and relabeling means switching columns). Well, these structures are very interesting, but I have to make a break here. I hope the pictures are inspiring enough.
--
Upcoming Paper: B. Steinbach, Ch. Posthoff: "Solution of the Last Open Four-Colored Rectangle-free Grid - an Extremely Complex Multiple-Valued Problem", 43rd International Symposium on Multiple-Valued Logic (2013), submitted.
18x18 Grid With Four Colors


Rectangle Free Four Coloring of 18x18 Grid, found by B. Steinbach and C. Posthoff
21x12 Grid With Four Colors


Rectangle Free Four Coloring of 21x12 Grid, found by B. Steinbach and C. Posthoff
 For a given complete bipartite graph K(m,n) you have to color its edges with c (e.g. c=4) colors. If you find a coloring such that there is no monochromatic rectangle in K(m,n) then you will have a rectangle free c-coloring of K(m,n). A grid is defined by the adjacency matrix of K(m,n). Each element is a number that indicates the edge color. Figures from above represents such a matrix with m=21 rows and n=12 columns. There are no four points forming a same colored rectangle such as you can see on the right figure.
For a given complete bipartite graph K(m,n) you have to color its edges with c (e.g. c=4) colors. If you find a coloring such that there is no monochromatic rectangle in K(m,n) then you will have a rectangle free c-coloring of K(m,n). A grid is defined by the adjacency matrix of K(m,n). Each element is a number that indicates the edge color. Figures from above represents such a matrix with m=21 rows and n=12 columns. There are no four points forming a same colored rectangle such as you can see on the right figure.The Zarankiewicz-Problem is a subproblem of the Grid Coloring Problem. Zarankiewicz asks for the minimum number of edges you have to insert into an empty bipartite graph such that there will be formed a rectangle as subgraph. Due to the pigeonhole principle the number of monochromatic edges of one color has to meet [mn/c] in the wanted four-coloring. If it does not then the Grid will not be c-colorable without monochromatic rectangles. Hence you have to solve the Zarankiewicz Problem for disproving a c-coloring of a grid.
B. Steinbach was able to solve the last open problems in the class of four-colorings (17x17, 17x18, 18x17, 18x18, 21x12), so he also found the bipartite Ramsey Number BR(2,4)=19 (similar to Ramsey Numbers, just take complete bipartite graphs with monochromatic bicliques). He worked together with Christian Posthoff on these problems. I was lucky to take part in this progress, even though I only was a witness. On one day I asked Bernd Steinbach again, if he had found some new results on the four coloring of the 21x12 problem. I knew that he again subjected a SAT solver to a very deep interrogation on the previous day. So Steinbach was speaking without any emotion about fifteen minutes that everything had been failed, what actually was the normal answer as always, and he finished with a little smile: "then he (SAT solver) got it".
First we really had our doubts and we were about to develop algorithms to prove that there could not be any 4-coloring. Well, my doubts were derived from Steinbach, admittedly I had no idea how to solve this problem. B. Steinbach created a very special sub-solution, which involved an ordered solution of the 21x12 Zarankiewicz-Problem, of course.
But the sub-solution was much more complicated. Steinbach explained it to me on the same day, but the "head" of that sub-solution looked very chaotic to me. After I understood I was stunned again by the system of chaos. O.k., I have to stop here for the sake of fairness. Steinbach will publish all the details on it soon but it will take some time. He did a great work, you will like it.
--
I have been playing around with the 21x12 solution to find the relationship between the color classes and the reduced latin squares of order 4, according to the Zarankiewicz Problem (see my upcoming paper). You will recognize the structure in the following pictures:




Each color class has been sorted, I use always the red color for the sake of readability. You also can see the Slot Architecture (matrix head (4,4,4) partition). The next figures show the structure of the four reduced latin squares in the adjacency matrix. One 3-bit pattern has to be expanded to three 2-bit patterns (see my upcoming paper).




As I worked out in my paper, the position of the last bits (highlighted) can be written in a tableau with four rows and four columns, so the Reduced Latin Squares of Order 4 are obtained:

The last three reduced latin squares belong to the same isotopy class (also isomorphic in this case, and relabeling means switching columns). Well, these structures are very interesting, but I have to make a break here. I hope the pictures are inspiring enough.
--
Upcoming Paper: B. Steinbach, Ch. Posthoff: "Solution of the Last Open Four-Colored Rectangle-free Grid - an Extremely Complex Multiple-Valued Problem", 43rd International Symposium on Multiple-Valued Logic (2013), submitted.
Labels:
12x21,
17x17,
18x18,
21x12 problem,
four coloring,
grid coloring,
monochromatic rectangle,
ramsey theory,
rectangle free,
reduced latin squares,
steinbach,
tu freiberg,
zarankiewicz
Zarankiewicz Problem and Algorithmic Approaches
Seminar Paper on Overflow Algorithm (english)
Download "An Algorithmic Approach for the Zarankiewicz Problem"
(formerly "Algorithmic Approaches for the Zarankiewicz Problem")
published at the 10th International Workshop on Boolean Problems:
(29.10.2012: Some corrections to the printed version, e.g. number of assignments with respect to row and column permutations)
Presentation on Overflow Algorithm (english)
Download Presentation Slides "An Algorithmic Approach for the Zarankiewicz Problem"
Seminar Paper (german)
Download "Algorithmische Betrachtungen zum Zarankiewicz-Problem"
(29.10.2012: "Solution of the Last Open Four-Colored Rectangle-free Grid" and "The Many Formulae for the Number of Latin Rectangles" added to list of literature)
(28.08.2012: number of assignments with respect to row and column permutations in section 1.2 corrected, Table 1.2 extended)
(31.05.2012: proof on relative runtime asymptotic estimation reworked)
(07.05.2012: time benchmarks on page 11 fixed due to "bug")
(13.03.12)
Overflow and Slot-Algorithm
Download Source Code in C++ // including getopt library by Ludvik Jerabek
(06.09.2012): small improvement on row incrementing (~5% speedup) and some code style
(07.05.2012: upper bounds for maximum of subgrids were partially wrong :/)
(13.03.2012)
// The solution matrix "PrevResults" does not contain the optimal value for 16x16 (unknown)
Seminar Paper - LaTeX/Gnuplot/processing
Download Source
(13.03.2012)
----------------------------------------------
Download "An Algorithmic Approach for the Zarankiewicz Problem"
(formerly "Algorithmic Approaches for the Zarankiewicz Problem")
published at the 10th International Workshop on Boolean Problems:
(29.10.2012: Some corrections to the printed version, e.g. number of assignments with respect to row and column permutations)
Presentation on Overflow Algorithm (english)
Download Presentation Slides "An Algorithmic Approach for the Zarankiewicz Problem"
Seminar Paper (german)
Download "Algorithmische Betrachtungen zum Zarankiewicz-Problem"
(29.10.2012: "Solution of the Last Open Four-Colored Rectangle-free Grid" and "The Many Formulae for the Number of Latin Rectangles" added to list of literature)
(28.08.2012: number of assignments with respect to row and column permutations in section 1.2 corrected, Table 1.2 extended)
(31.05.2012: proof on relative runtime asymptotic estimation reworked)
(07.05.2012: time benchmarks on page 11 fixed due to "bug")
(13.03.12)
Overflow and Slot-Algorithm
Download Source Code in C++ // including getopt library by Ludvik Jerabek
(06.09.2012): small improvement on row incrementing (~5% speedup) and some code style
(07.05.2012: upper bounds for maximum of subgrids were partially wrong :/)
(13.03.2012)
// The solution matrix "PrevResults" does not contain the optimal value for 16x16 (unknown)
Seminar Paper - LaTeX/Gnuplot/processing
Download Source
(13.03.2012)
----------------------------------------------
During the last few months I have been working on the Zarankiewicz Problem for my seminar paper. My part was to develop some algorithms, and initially I was supposed to do this using CUDA. After some trials I decided to return to the CPU side, because the problem comes from the extremal graph theory. As far as I know it is even a problem to find the locality of such problems. Actually it even was difficult for me to write a decent and exact algorithm on the CPU side.
In my work you will find two algorithms. The first one is the Overflow Algorithm which works non-recursively and returns the global maximum of edges of the C4-saturated subgraph of K(m,n) (complete bipartite graph). Furthermore I show some ideas for optimization, but they are too savagely and make the algorithm inaccurate. Nevertheless, some nice structure information leads to an interesting connection with the slot architecture of the second algorithm.
The second algorithm is a greedy one called Slot Algorithm. The key idea is from B. Steinbach; he is my supervisor in this work. Different structure information had been used, however, the problem insists to be a beast. I could not finish the Slot Algorithm as I would have liked to do. There are many open questions about the bit/edge pattern hierarchy and how bit patterns of different sizes interact with each other.
Related Posts:
Rectangle Free Grid Coloring of 21x12
In my work you will find two algorithms. The first one is the Overflow Algorithm which works non-recursively and returns the global maximum of edges of the C4-saturated subgraph of K(m,n) (complete bipartite graph). Furthermore I show some ideas for optimization, but they are too savagely and make the algorithm inaccurate. Nevertheless, some nice structure information leads to an interesting connection with the slot architecture of the second algorithm.
The second algorithm is a greedy one called Slot Algorithm. The key idea is from B. Steinbach; he is my supervisor in this work. Different structure information had been used, however, the problem insists to be a beast. I could not finish the Slot Algorithm as I would have liked to do. There are many open questions about the bit/edge pattern hierarchy and how bit patterns of different sizes interact with each other.
Related Posts:
Rectangle Free Grid Coloring of 21x12
Abonnieren
Posts (Atom)
